¿Qué es un vector?
Se llama vector a un segmento de recta en el espacio que parte de un punto hacia otro, es decir, que tiene dirección y sentido .Los vectores se representan gráficamente con una flecha. Así mismo, cuando deben ser expresados en una fórmula, se representan con una letra coronada por una flecha.
Ejemplo 1:
Ejemplo 2:
Magnitudes Vectoriales
Las magnitudes vectoriales son aquellas que, además de representarse con un número y una unidad, requieren también ser expresadas en el espacio con una dirección y un sentido, es decir, con un vector. Esto las distingue de las magnitudes escalares, las cuales solo requieren un número y una unidad.
La magnitud de un vector 
es la distancia entre el punto inicial P y el punto final Q . En símbolos la magnitud de es escrita como 
.
es la distancia entre el punto inicial P y el punto final Q . En símbolos la magnitud de es escrita como .
Si las coordenadas del punto inicial y del punto final de un vector están dadas, la fórmula de la distancia puede ser usada para encontrar su magnitud.
Ejemplo:Encuentre la magnitud del vector cuyo punto inicial P está en (1, 1) y punto final es Q y está en (5, 3).
cuyo punto inicial P está en (1, 1) y punto final es Q y está en (5, 3).
Solución: Use la formula de la distancia. Sustituya los valores de x 1 , y 1 , x 2 , y y 2 .
La magnitud de es alrededor de 4.5.
es alrededor de 4.5.Dirección de un vector
La dirección de un vector es la medida del ángulo que hace con una línea horizontal. Una de las fórmulas siguientes puede ser usada para encontrar la dirección de un vector:
, donde x es el cambio horizontal y y es el cambio vertical o
, donde ( x 1 , y 1 ) es el punto inicial y ( x 2 , y 2 ) es el punto terminal.
Ejemplo :
Encuentre la dirección del vector cuyo punto inicial P está en (2, 3) y punto final Q está en (5, 8).
cuyo punto inicial P está en (2, 3) y punto final Q está en (5, 8).
Las coordenadas del punto inicial y del punto terminal están dadas. Sustitúyalos en la fórmula .
.
Encuentre la tan inversa, luego use una calculadora.
El vector tiene una dirección de alrededor 59.
tiene una dirección de alrededor 59.Características de los vectores
Los componentes de los vectores que definen sus características son los siguientes:
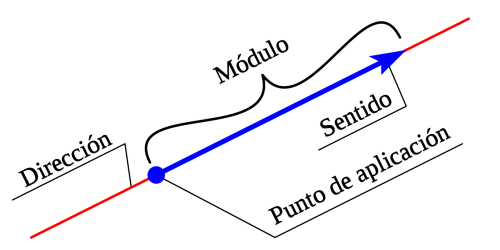
- Modulo o Magnitud : Se refiere a la longitud o amplitud del vector o segmento de recta.
- Dirección: Se refiere a la inclinación que posee el vector con respecto a un eje horizontal imaginario, con el cual forma un angulo.
- Sentido : Se refiere a la orientación del vector, indicado por la cabeza de la flecha del vector. Puede ser positivo ( + ) o negativo ( - ).
Tipos de vectores
- Vectores Nulos: Son aquellos donde origen y extremo coinciden y, por lo tanto, el modulo o magnitud es igual a 0. Por ejemplo.
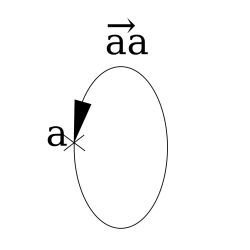
- Vectores Unitarios: Son aquellos cuyo modulo es igual a 1. Por ejemplo:
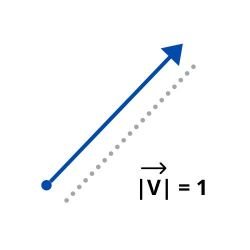
- Vectores Fijos: Son aquellos que expresan un punto de origen ademas de un extremo, el cual esta determinado en un punto fijo del espacio. Suelen usarse, por ejemplo: para expresar la fuerza aplicada sobre dicho punto.Para representarlos. se dice que el punto de origen es A y el extremo es B. ejemplo:
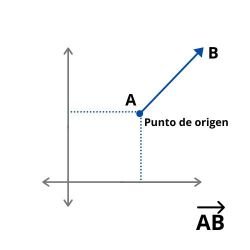
- Vectores paralelos: Están situados en rectas paralelas, pero poseen un mismo sentido o contrario. Por ejemplo:
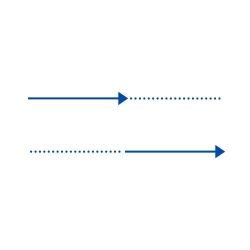
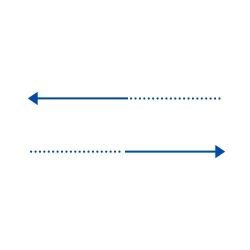
- Vectores Opuestos: Se caracterizan por tener la misma dirección y magnitud , pero su sentido es opuesto. Por ejemplo.
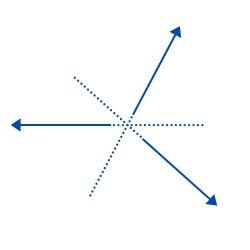
- Vectores concurrentes o angulares: Son aquellos cuyas lineas de acción pasan por el mismo punto, es decir, se intercaran. Por ejemplo:
- Vectores libres: Son aquellos vectores cuyo punto de aplicación es indeterminado y, por lo tanto, libre. Por ejemplo:
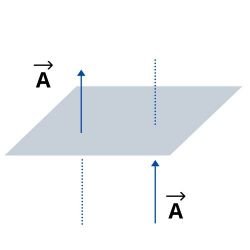
- Vectores equipolentes o iguales: Son aquellos vectores con igual modulo, dirección y sentido. Por ejemplo:
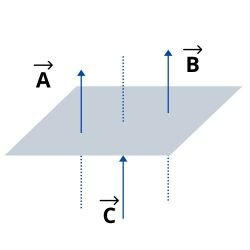
- Vectores Coplanarios: Son aquellos que están en un mismo plano. Por ejemplo:
- Vectores colegiales: sus líneas de acción se encuentran sobre una misma recta. Por ejemplo:
- Vectores axiales o pseudovectores: son los que están ligados a efectos de giro. La dirección señala el eje de rotación del segmento. Por ejemplo:
